Distancia entre dos puntos
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x 2 – x 1 ) .
Si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
Ejemplos:
ejemplo 1:
Calcular la distancia entre los siguientes puntos:
Aplicamos directamente la fórmula anterior o lo que es lo mismo, calculando el módulo del vector AB:
Ahora operamos y obtenemos la distancia entre esos dos puntos, que es de 5 unidades:
ejemplo 2:
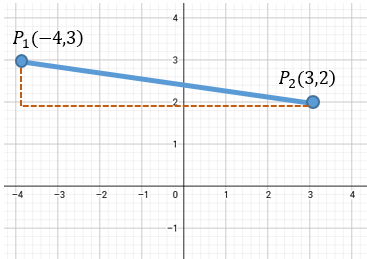
Hallar la distancia entre los puntos P1 (-4, 3) y P2 (3, 2)
Elegimos cualquier punto, puede ser el Punto 1, o puede ser el Punto 2. No importa a quién tomemos como inicial, el resultado debe ser el mismo. En este caso vamos elegir al punto uno como inicial, y punto dos como final.
De nuestra fórmula:
Ejercicios a resolver:
1.- Encuentre la distancia entre los puntos siguientes, considere el par ordenado P1 (-2, 3) y P2 (3,3).
2.- Hallar la distancia entre los puntos P1 (-5, 3) y P2 (4, 3).
VÍDEO EN EL QUE TE PUEDES APOYAR:
Biografía:
https://www.fisimat.com.mx/distancia-entre-dos-puntos/
https://www.geoan.com/vectores/distancia.html
https://www.cecyt3.ipn.mx/ibiblioteca/mundodelasmatematicas/DistanciaEntreDosPuntos.html
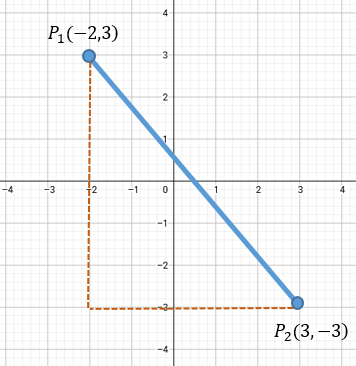



No hay comentarios:
Publicar un comentario